What concepts or facts do you know from math that is mind blowing, awesome, or simply fascinating?
Here are some I would like to share:
- Gödel’s incompleteness theorems: There are some problems in math so difficult that it can never be solved no matter how much time you put into it.
- Halting problem: It is impossible to write a program that can figure out whether or not any input program loops forever or finishes running. (Undecidablity)
The Busy Beaver function
Now this is the mind blowing one. What is the largest non-infinite number you know? Graham’s Number? TREE(3)? TREE(TREE(3))? This one will beat it easily.
- The Busy Beaver function produces the fastest growing number that is theoretically possible. These numbers are so large we don’t even know if you can compute the function to get the value even with an infinitely powerful PC.
- In fact, just the mere act of being able to compute the value would mean solving the hardest problems in mathematics.
- Σ(1) = 1
- Σ(4) = 13
- Σ(6) > 101010101010101010101010101010 (10s are stacked on each other)
- Σ(17) > Graham’s Number
- Σ(27) If you can compute this function the Goldbach conjecture is false.
- Σ(744) If you can compute this function the Riemann hypothesis is false.
Sources:
- YouTube - The Busy Beaver function by Mutual Information
- YouTube - Gödel’s incompleteness Theorem by Veritasium
- YouTube - Halting Problem by Computerphile
- YouTube - Graham’s Number by Numberphile
- YouTube - TREE(3) by Numberphile
- Wikipedia - Gödel’s incompleteness theorems
- Wikipedia - Halting Problem
- Wikipedia - Busy Beaver
- Wikipedia - Riemann hypothesis
- Wikipedia - Goldbach’s conjecture
- Wikipedia - Millennium Prize Problems - $1,000,000 Reward for a solution
I came here to find some cool, mind-blowing facts about math and have instead confirmed that I’m not smart enough to have my mind blown. I am familiar with some of the words used by others in this thread, but not enough of them to understand, lol.
Please feel free to ask any questions! Math is a wonderful field full of beauty but unfortunately almost all education systems fail to show this and instead makes it seem like raw robotic calculations instead of creativity.
Math is best learned visually and with context to more abstract terms. 3Blue1Brown is the best resource in my opinion for this!
Here’s a mindblowing fact for you along with a video from 3Blue1Brown. Imagine you are sliding a 1,000,000 kg box and slamming it into a 1 kg box on an ice surface with no friction. The 1 kg box hits a wall and bounces back to hit the 1,000,000 kg box again.
The number of bounces that appear is the digits of Pi. Crazy right? Why would pi appear here? If you want to learn more here’s a video from the best math teacher in the world.
Thanks! I appreciate the response. I’ve seen some videos on 3blue1brown and I’ve really enjoyed them. I think if I were to go back and fill in all the blank spots in my math experience/education I would enjoy math quite a bit.
Same here! Great post but I’m out! lol
Nonsense! I can blow both your minds without a single proof or mathematical symbol, observe!
There are different sizes of infinity.
Think of integers, or whole numbers; 1, 2, 3, 4, 5 and so on. How many are there? Infinite, you can always add one to your previous number.
Now take odd numbers; 1, 3, 5, 7, and so on. How many are there? Again, infinite because you just add 2 to the previous odd number and get a new odd number.
Both of these are infinite, but the set of numbers containing odd numbers is by definition smaller than the set of numbers containing all integers, because it doesn’t have the even numbers.
But they are both still infinite.
I may be wrong or have misunderstood what you said but the sets of natural numbers and odd numbers have the same size/cardinality. If there exists a bijection between the two sets then they have the same size.
f(x) = 2x + 1 is such a bijection
For the same reason, N, Z and Q have the same cardinality. The fact that each one is included in the next ones doesn’t mean their size is different.
Agree. Uncountable infinities are much more mind blowing. It was an interesting journey realising first that everything like time and distance are continuous when learning math the then realising they’re not when learning physics.
Your fact is correct, but the mind-blowing thing about infinite sets is that they go against intuition.
Even if one might think that the number of odd numbers is strictly less than the number of all natural numbers, these two sets are in fact of the same size. With the mapping n |-> 2*n - 1 you can map each natural number to a different odd number and you get every odd number with this (such a function is called a bijection), so the sets are per definition of the same size.
To get really different “infinities”, compare the natural numbers to the real numbers. Here you can’t create a map which gets you all real numbers, so there are “more of them”.
There was a response I left in the main comment thread but I’m not sure if you will get the notification. I wanted to post it again so you see it
Response below
Please feel free to ask any questions! Math is a wonderful field full of beauty but unfortunately almost all education systems fail to show this and instead makes it seem like raw robotic calculations instead of creativity.
Math is best learned visually and with context to more abstract terms. 3Blue1Brown is the best resource in my opinion for this!
Here’s a mindblowing fact for you along with a video from 3Blue1Brown. Imagine you are sliding a 1,000,000 kg box and slamming it into a 1 kg box on an ice surface with no friction. The 1 kg box hits a wall and bounces back to hit the 1,000,000 kg box again.
The number of bounces that appear is the digits of Pi. Crazy right? Why would pi appear here? If you want to learn more here’s a video from the best math teacher in the world.
That’s so cool! Thanks for the reply and the link.
11 X 11 = 121
111 X 111 = 12321
1111 X 1111 = 1234321
11111 X 11111 = 123454321
111111 X 1111111 = 12345654321
holt shit
You could include 1 x 1 = 1
But thats so cool. Maths is crazy.
Amazing in deed!
Just a small typo in the very last factor
1111111.
The four-color theorem is pretty cool.
You can take any map of anything and color it in using only four colors so that no adjacent “countries” are the same color. Often it can be done with three!
Maybe not the most mind blowing but it’s neat.
Thanks for the comment! It is cool and also pretty aesthetically pleasing!

If you had a 3 dimensional map, would you need more colors to achieve the same results?
Edit: it was explained in your link. It looks like for surfaces in 3D space, this can’t be generalized.
What about a hypothetical country that is shaped like a donut, and the hole is filled with four small countries? One of the countries must have the color of one of its neighbors, no?

There are some rules about the kind of map this applies to. One of them is “no countries inside other countries.”
I see.
Not true, see @BitSound’s comment.
It does have to be topologically planar (may not be the technical term), though. No donut worlds.
The regions need to be contiguous and intersect at a nontrivial boundary curve. This type of map can be identified uniquely with a planar graph by placing a vertex inside each region and drawing an edge from one point to another in each adjacent region through the bounding curve.
I think the four small countries inside would each only have 2 neighbours. So you could take 2 that are diagonal and make them the same colour.
But each small country has three neighbors! Two small ones, and always the big donut country. I attached a picture to my previous comment to make it more clear.
In your example the blue country could be yellow and that leaves the other yellow to be blue. Now no identical colors touch.
You still have two red countries touching each other, what are you talking about?
Oops I meant the red one goes blue.
Whoops I should’ve been clearer I meant two neighbours within the donut. So the inside ones could be 2 or 3 colours and then the donut is one of the other 2 or the 1 remaining colour.
You’re right. Bad example from my side. But imagine this scenario:

Make purple yellow and one of the reds purple.
…There is no purple though?
That map is actually still quite similar to the earlier example where all 4 donut hole countries are the same. Once again on the right is the adjacency graph for the countries where I’ve also used a dashed line to show the only difference in adjacency.
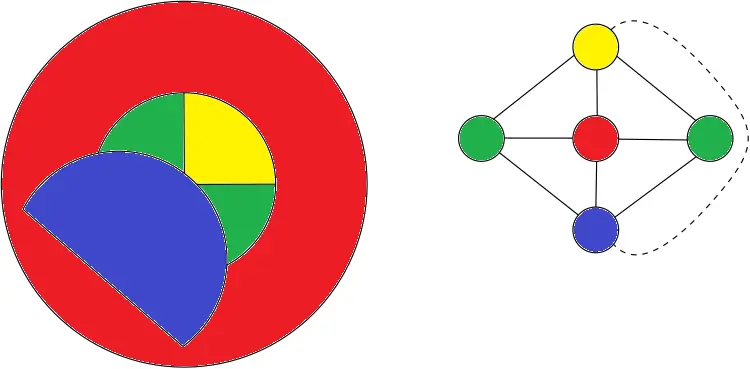
Oh wow, now I feel dumb. Thanks.
 Ok now do this one. What color is the donut country?
Ok now do this one. What color is the donut country?Someone beat me to it, so I thought I’d also include the adjacency graph for the countries, it can be easier to see the solution to colouring them.
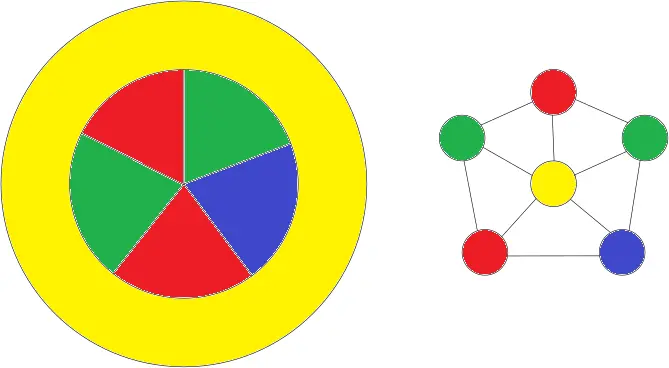

Looks to be that way one of the examples given on the wiki page. It is still however an interesting theory, if four countries touching at a corner, are the diagonal countries neighbouring each other or not. It honestly feels like a question that will start a war somewhere at sometime, probably already has.
In graph theory there are vertices and edges, two shapes are adjacent if and only if they share an edge, vertices are not relevant to adjacency. As long as all countries subscribe to graph theory we should be safe
The only problem with that it that it requires all countries to agree to something, and that seems to become harder and harder nowadays.
In that image, you could color yellow into purple since it’s not touching purple. Then, you could color the red inner piece to yellow, and have no red in the inner pieces.
Isn’t the proof of this theorem like millions of pages long or something (proof done by a computer ) ? I mean how can you even be sure that it is correct ? There might be some error somewhere.
deleted by creator
Which one?
deleted by creator
Not so much a fact, but I’ve always liked the prime spirals: https://en.wikipedia.org/wiki/Ulam_spiral
Also, not as impressive as the busy beaver, but Knuth’s up-arrow notation is cool: https://en.wikipedia.org/wiki/Knuth’s_up-arrow_notation
Knuth’s arrow shows up in… Magic the Gathering. There’s a challenge of “how much damage can you deal with just 3 cards and without infinitely repeating loops?”. Turns out that stacking doubler effects can get us really high. https://www.polygon.com/23589224/magic-phyrexia-all-will-be-one-best-combo-attacks-tokens-vindicator-mondrak
deleted by creator
maybe this will make more sense when I watch the veritasium video, but I don’t have time to do that until the weekend. How is 3x+1 unprovable? won’t all odd numbers multiplied by 3 still be odd? and won’t adding 1 to an odd number always make it even? and aren’t all even numbers by definition divisible by 2? I’m struggling to see how there could be any uncertainty in this
deleted by creator
The unproven part is that it eventually will reach 1, not that it’s not possible to do the computation. Someone may find a number loop that doesn’t eventually reach 1.
Just after going through a few examples in my head, the difficulty becomes somewhat more apparent. let’s start with 3. This is odd, so 3(3)+1 = 10. 10 is even so we have 10/2=5.
By this point my intuition tells me that we don’t have a very obvious pattern that we can use to decide whether the function will output 4, 2, or 1 by recursively applying the function to its own output, other than the fact that every other number that we try appears to result in this pattern. We could possibly reduce the problem to whether we can guess that the function will eventually output a power of 2, but that doesn’t sound to me like it makes things much easier.
If I had no idea whether a proof existed, I would guess that it may, but that it is non-trivial. Or at least my college math courses did not prepare me to find one. Since it looks like plenty of professional mathematicians have struggled with it, I have no doubt that if a proof exists it is non-trivial.
The one I bumped into recently: the Coastline Paradox
“The coastline paradox is the counterintuitive observation that the coastline of a landmass does not have a well-defined length. This results from the fractal curve–like properties of coastlines; i.e., the fact that a coastline typically has a fractal dimension.”
For me, personally, it’s the divisible-by-three check. You know, the little shortcut you can do where you add up the individual digits of a number and if the resulting sum is divisible by three, then so is the original number.
That, to me, is black magic fuckery. Much like everything else in this thread I have no idea how it works, but unlike everything else in this thread it’s actually a handy trick that I use semifrequently
That one’s actually really easy to prove numerically.
Not going to type out a full proof here, but here’s an example.
Let’s look at a two digit number for simplicity. You can write any two digit number as 10*a+b, where a and b are the first and second digits respectively.
E.g. 72 is 10 * 7 + 2. And 10 is just 9+1, so in this case it becomes 72=(9 * 7)+7+2
We know 9 * 7 is divisible by 3 as it’s just 3 * 3 * 7. Then if the number we add on (7 and 2) also sum to a multiple of 3, then we know the entire number is a multiple of 3.
You can then extend that to larger numbers as 100 is 99+1 and 99 is divisible by 3, and so on.
Waaaait a second.
Does that hold for every base, where the divisor is 1 less than the base?
Specifically hexidecimal - could it be that 5 and 3 have the same “sum digits, get divisibility” property, since 15 (=3*5) is one less than the base number 16?
Like 2D16 is16*2+13 = 45, which is divisible by 3 and 5.
Can I make this into a party trick?! “Give me a number in hexidecimal, and I’ll tell you if it’s divisible by 10.”
Am thinking it’s 2 steps:
- Does it end with a 0, 2, 4, 6, 8, A, C, E? Yes means divisible by 2.
- Do the digits add up to a multiple of 5 (ok to subtract 5 liberally while adding)? Skip A and F. For B add 1; C->2, D->3, E->4. If the sum is divisible by 5, then original number is too.
So if 1 and 2 are “yes”, it’s divisible by 10.
E.g.
- DEADBAE16 (=23349547010): (1) ends with E, ok. (2) 3+4+3+1+4=15, divisible by 5. Both are true so yes, divisible by 10.
- C4744416 (=1287482010): (1) ends with 4, ok. (2) 2+4+7+4+4+4=25, ok.
- BEEFFACE16 (=3203398350): (1) E, ok. (2) 1+4+4+2+4=15, ok.
Is this actually true? Have I found a new party trick for myself? How would I even know if this is correct?
How would I even know if this is correct?
You’re gonna have to go to a lot of parties
A simple one: Let’s say you want to sum the numbers from 1 to 100. You could make the sum normally (1+2+3…) or you can rearrange the numbers in pairs: 1+100, 2+99, 3+98… until 50+51 (50 pairs). So you will have 50 pairs and all of them sum 101 -> 101*50= 5050. There’s a story who says that this method was discovered by Gauss when he was still a child in elementary school and their teacher asked their students to sum the numbers.
Goldbach’s Conjecture: Every even natural number > 2 is a sum of 2 prime numbers. Eg: 8=5+3, 20=13+7.
https://en.m.wikipedia.org/wiki/Goldbach’s_conjecture
Such a simple construct right? Notice the word “conjecture”. The above has been verified till 4x10^18 numbers BUT no one has been able to prove it mathematically till date! It’s one of the best known unsolved problems in mathematics.
How can you prove something in math when numbers are infinite? That number you gave if it works up to there we can call it proven no? I’m not sure I understand
As you said, we have infinite numbers so the fact that something works till 4x10^18 doesn’t prove that it will work for all numbers. It will take only one counterexample to disprove this conjecture, even if it is found at 10^100. Because then we wouldn’t be able to say that “all” even numbers > 2 are a sum of 2 prime numbers.
So mathematicians strive for general proofs. You start with something like: Let n be any even number > 2. Now using the known axioms of mathematics, you need to prove that for every n, there always exists two prime numbers p,q such that n=p+q.
Would recommend watching the following short and simple video on the Pythagoras theorem, it’d make it perfectly clear how proofs work in mathematics. You know the theorem right? For any right angled triangle, the square of the hypotenuse is equal to the sum of squares of both the sides. Now we can verify this for billions of different right angled triangles but it wouldn’t make it a theorem. It is a theorem because we have proved it mathematically for the general case using other known axioms of mathematics.
There are many structures of proof. A simple one might be to prove a statement is true for all cases, by simply examining each case and demonstrating it, but as you point out this won’t be useful for proving statements about infinite cases.
Instead you could assume, for the sake of argument, that the statement is false, and show how this leads to a logical inconsistency, which is called proof by contradiction. For example, Georg Cantor used a proof by contradiction to demonstrate that the set of Natural Numbers (1,2,3,4…) are smaller than the set of Real Numbers (which includes the Naturals and all decimal numbers like pi and 69.6969696969…), and so there exist different “sizes” of infinity!
For a method explicitly concerned with proofs about infinite numbers of things, you can try Proof by Mathematical Induction. It’s a bit tricky to describe…
- First demonstrate that a statement is true in some 1st base case.
- Then demonstrate that if it holds true for the abstract Nth case, then it necessarily holds true for the (N+1)th case (by doing some clever rearranging of algebra terms or something)
- Therefore since it holds true for the 1th case, it must hold true for the (1+1)th case = the 2th case. And since it holds true for the 2th case it must hold true for the (2+1)=3th case. And so on ad infinitum.
Wikipedia says:
Mathematical induction can be informally illustrated by reference to the sequential effect of falling dominoes.
Bear in mind, in formal terms a “proof” is simply a list of true statements, that begin with axioms (which are true by default) and rules of inference that show how each line is derived from the line above.
Just to add to this. Another way could be to find a specific construction. If you could for example find an algorithm that given any even integer returns two primes that add up to it and you showed this algorithm always works. Then that would be a proof of the Goldbach conjecture.
Very cool and fascinating world of mathematics!
Wtf !
x^n + y^n = z^n has no solutions where n > 2 and x, y and z are all natural numbers. It’s hard to believe that, knowing that it has an infinite number of solutions where n = 2.
Pierre de Format, after whom this theorem was named, famously claimed to have had a proof by leaving the following remark in some book that he owned: “I have a proof of this theorem, but there is not enough space in this margin”. It took mathematicians several hundred years to actually find the proof.
e^(pi i) = -1
like, what?
If you think of complex numbers in their polar form, everything is much simpler. If you know basic calculus, it can be intuitive.
Instead of z = + iy, write z = (r, t) where r is the distance from the origin and t is the angle from the positive x-axis. Now addition is trickier to write, but multiplication is simple: (a,b) * (c,d) = (ab, b + d). That is, the lengths multiply and the angles add. Multiplication by a number (1, t) simply adds t to the angle. That is, multiplying a point by (1, t) is the same as rotating it counterclockwise about the origin by an angle t.
The function f(t) = (1, t) then parameterizes a circular motion with a constant radial velocity t. The tangential velocity of a circular motion is perpendicular to the current position, and so the derivative of our function is a constant 90 degree multiple of itself. In radians, that means f’(t) = (1, pi/2)f(t). And now we have one of the simplest differential equations whose solution can only be f(t) = k * e^(t* (1, pi/2)) = ke^(it) for some k. Given f(0) = 1, we have k = 1.
All that said, we now know that f(t) = e^(it) is a circular motion passing through f(0) = 1 with a rate of 1 radian per unit time, and e^(i pi) is halfway through a full rotation, which is -1.
If you don’t know calculus, then consider the relationship between exponentiation and multiplication. We learn that when you take an interest rate of a fixed annual percent r and compound it n times a year, as you compound more and more frequently (i.e. as n gets larger and larger), the formula turns from multiplication (P(1+r/n)^(nt)) to exponentiation (Pe^(rt)). Thus, exponentiation is like a continuous series of tiny multiplications. Since, geometrically speaking, multiplying by a complex number (z, z^(2), z^(3), …) causes us to rotate by a fixed amount each time, then complex exponentiation by a continuous real variable (z^t for t in [0,1]) causes us to rotate continuously over time. Now the precise nature of the numbers e and pi here might not be apparent, but that is the intuition behind why I say e^(it) draws a circular motion, and hopefully it’s believable that e^(i pi) = -1.
All explanations will tend to have an algebraic component (the exponential and the number e arise from an algebraic relationship in a fundamental geometric equation) and a geometric component (the number pi and its relationship to circles). The previous explanations are somewhat more geometric in nature. Here is a more algebraic one.
The real-valued function e^(x) arises naturally in many contexts. It’s natural to wonder if it can be extended to the complex plane, and how. To tackle this, we can fall back on a tool we often use to calculate values of smooth functions, which is the Taylor series. Knowing that the derivative of e^(x) is itself immediately tells us that e^(x) = 1 + x + x^(2)/2! + x^(3)/3! + …, and now can simply plug in a complex value for x and see what happens (although we don’t yet know if the result is even well-defined.)
Let x = iy be a purely imaginary number, where y is a real number. Then substitution gives e^x = e^(iy) = 1 + iy + i(2)y(2)/2! + i(3)y(3)/3! + …, and of course since i^(2) = -1, this can be simplified:
e^(iy) = 1 + iy - y^(2)/2! - iy^(3)/3! + y^(4)/4! + iy^(5)/5! - y^(6)/6! + …
So we’re alternating between real/imaginary and positive/negative. Let’s factor it into a real and imaginary component: e^(iy) = a + bi, where
a = 1 - y^(2)/2! + y^(4)/4! - y^(6)/6! + …
b = y - y^(3)/3! + y^(5)/5! - y^(7)/7! + …
And here’s the kicker: from our prolific experience with calculus of the real numbers, we instantly recognize these as the Taylor series a = cos(y) and b = sin(y), and thus conclude that if anything, e^(iy) = a + bi = cos(y) + i sin(y). Finally, we have e^(i pi) = cos(pi) + i sin(pi) = -1.
Damn that’s actually pretty simple way to use differential equations to show this.
Edit. The series one is also pretty simple.
3Blue 1Brown actually explains that one in a way that makes it seem less coincidental and black magic. Totally worth a watch
As an engineer, i dont know how to feel about this. On the one hand, 19.99999 = 20. But on the other hand, 3^3 - 3 = 24.
Oh fuck you. I’m going to insert this in place of 20 in some formula and see people have breakdowns.
you need a space before the second pi
The birthday paradox
Small nit: you don’t compute sigma, you prove a value for a given input. Sigma here is uncomputable.
was not aware of the machines halting only iff conjectUres are true, tho. Thats a flat out amazing construction.









